LLMs struggle with perception, not reasoning, in ARC-AGI

What made o3 so much better than previous models on this benchmark?

On Friday, OpenAI announced their new o3 reasoning model, solving an extremely impressive 366/400 tasks in the ARC-AGI-Pub dataset. I published a visualization of the tasks that o3 couldn’t solve; you can see those examples, and get a feel for the hardest ARC tasks, here:

o3 and ARC-AGI: The unsolved tasks

There were a number of different failure modes seen that data, but as some of you observed, there were a number of cases where o3 appeared to be struggling with the data format rather than understanding the task itself.

I’d like to draw attention to a pattern I’ve noticed since we started looking at the first generation of LLMs last year, and which might explain some of what we’ve seen on ARC this year.

Task length is everything

One of the unique aspects of ARC is that the tasks come in many shapes and sizes - each has a variable number of examples and a rectangular output size between 1x1 and 30x30 pixels. This is in service of its goal to present 400 unique reasoning challenges, each problem requiring some different intuition within roughly some core knowledge principles.

o3 does extremely well at ARC overall, but it gets interesting when we stratify ARC solve rates by problem size (total number of pixels in the training grids¹):

Task solve rates (ARC-AGI-Pub) by various models. Each point represents a sliding window of tasks with length in the range [l/2,l*2], with bootstrapped 75% CI shaded.

What we see is quite striking: LLMs are really good at solving the smallest ARC tasks, even prior to o3. Each subsequent model gets better and better at solving larger tasks, but everything before o3 (and especially pre-o1) struggles with solving tasks with >512 input pixels. With o3, we raise that threshold to perhaps 4096 input pixels.

Now, we can look at the other side of this coin; the distribution of ARC:

Count of tasks with a length in the range [l/2, l*2] at each point. This represents the weighting of each point in the previous figure to the overall ARC performance: it mostly depends on tasks between 512-2048 pixels.

The majority of tasks are clustered around 1024 pixels - so if you build a model that is able to reason on digit grid problems above this size, you get a threshold effect that means you can solve most ARC tasks! If you struggle to do any reasoning on problems this size, your score is guaranteed to be poor, and that’s what we’ve seen until o1 (and now o3).

But surely this performance difference is explained by the fact that the bigger tasks require more reasoning and o3 is better at that reasoning - right?

Humans do this differently

Perhaps we can say that ‘reasoning difficulty’ corresponds with how hard it is for a human to get it right. This means we can look at human solve rates for these tasks as a proxy for reasoning difficulty.

The H-ARC paper released this year tested every ARC task on an average of 10 Mechanical Turk users - and so we can stratify these solve rates like we did for LLMs.

Task solve rates (ARC-AGI-Pub) of the average human participant in H-ARC. When compared to the first figure, there is no sign of a major drop-off across tasks. The CI is smaller as each task was attempted by several participants.

What we see is that the difficulty of a task for a human doesn’t depend on the size of the grid! Some tasks are easy, some tasks are hard, but rather than struggling with the literal size of the problem, humans struggle with other aspects.

We also see that o3 is superhuman (at least the average human²) on small tasks - but worse than humans on the largest tasks.

Indeed, the H-ARC paper itself talks about how the ARC evaluation set is more difficult for people than the training set, and that this doesn’t seem to be a caused by grid size of the ARC problems:

Although it is still unclear why […], our results suggest that factors other than output grid size are contributing to difficulty on the evaluation set and that for equally sized output grids, evaluation tasks are still often more difficult than training tasks. We suspect that the primitive operations underlying the transformations for evaluation tasks are more difficult to infer and/or execute than in the training set.

LLMs are not naturally suited for ARC

A lot of this likely comes down to the fact that text is a very contrived format for ARC to be solved in. Here’s the format that OpenAI uses for giving tasks to LLMs:

OpenAI’s prompt format, tokenized. Each pixel becomes a single with a space token in-between (although it’s always possible o3 uses a different tokenizer).

ARC is fundamentally a 2D problem, and requires reasoning across both rows and columns. Since LLMs consume and produce tokens in a 1D format, this means that reasoning across columns requires combining information across longer contexts.

We saw in our previous work that allowing LLMs like LLaMA and GPT-4 to attempt ARC tasks in both row-major and column-major formats can as much as double performance³, as tasks that require reasoning over columns become much easier when presented in column-major format.

With this 1D format, tasks requiring skills like object recognition become much more challenging as you have to correlate digits across multiple rows that might be 60 tokens apart - we saw o3 failing on such object recognition a couple times. What’s more, you have to output up to 1800 tokens of response without making any grid alignment mistakes (in several cases, o3 clearly ‘had the right idea’ but failed to output a correctly sized grid or skipped a row).

Two tasks that o3 failed due to being unable to output a 30x30 grid at all, despite millions of reasoning tokens and 1024 ‘samples’ (likely majority voting). On the left, a row is skipped both times; on the right, erroneous pixels are added in some rows.

As the grids get larger, reasoning over longer contexts is required, and digits further apart must be combined and reasoned upon (with exact precision). With models smaller than o3, this becomes even more apparent.

An example of larger LLMs getting better at outputting a coherent grid. White pixels represent where the model outputted different-size rows.

LLMs hate this one simple trick

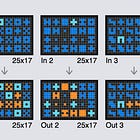
We can test this hypothesis by comparing how models handle the same-difficulty problem at different grid sizes. One avenue is to transform each task into an enlarged ARC task by duplicating every column and row. Here’s a task that o1-mini solves, along with its enlarged cousin:

I’d say the two tasks are pretty similar in difficulty, at least in the difficulty axis that ARC is designed to measure. But o1-mini is consistently unable to solve the latter!

Three tasks perfectly solved by o1-mini, but where it fails on the enlarged version. In the first example, o1-mini is unable to produce the 30x30 grid at all.

In fact, of 39 ARC-AGI-Pub tasks that o1-mini solved first-try in my testing, it could only solve 8 of the corresponding enlarged tasks.⁴

We know this isn’t that LLMs can’t generalise the transformation from only 3-5 examples, because it just demonstrably did on the normal tasks. But when the grids are too large, the model is either failing to understand the task at all, or failing to output the right answer.

What does this mean for the benchmark?

It appears that specifically in the case of LLMs, ARC is acting as a “grid perception and transformation” benchmark as well as a general reasoning/intelligence benchmark, and thus might overstate some improvements and understate others. Understanding ARC within an LLM requires modelling complex interactions between many far-away tokens and applying precise nonlinear transforms - but is this really testing ‘the ability to efficiently acquire new skills outside of its training data’ in the way ARC is intended to?⁵

There are two particular implications that come to mind:

1. The innate reasoning abilities of previous LLMs may be understated, or at least poorly measured, by ARC, due to the challenges of abstracting and reasoning on large 2D grids in text form.

2. The tremendous gain of OpenAI's o3 may be overstated by ARC, because it's the first model able to operate on pixel grids of problem length that ARC happens to exist in (a threshold effect).

I heard a nice analogy at NeurIPS that giving 2D ARC tasks to an LLM is like expecting humans to perform reasoning in 4D - this is a reasonable point⁶. However, is this a defect of the benchmark or of the LLM? It's not unreasonable to expect an AGI to be general enough to scale to these sorts of problems.

Further, if LLMs are constrained by their ability to apply reasoning to long sequences of digits, what does this say about scaling them to AGI? Do we need to provide better tools for such systems to abstract concepts from structured input and reverse them back out without making mistakes (in the way that humans, or indeed more traditional program induction methods, make quick work of?) How can we scale these methods to give them more invariances that people have, and can this allow us to solve ARC for less than a million dollars?

I’d love to hear your thoughts on all these questions, either in the comments, or on Twitter. Let me know what you think!

---

Thanks to Anastasia Courtney and Max McGuinness for reviewing and bouncing ideas.

1. This choice is somewhat arbitrary, for example the same effect is visible if you instead look at the size of each training example (divide by number of examples).

2. And at least the average human motivated monetarily on Mechanical Turk, where there might be an incentive to complete tasks quickly rather than well. Individual tasks still seem to have a hardness to them, just not very associated with size (it’s not that every task has 25% of respondents intentionally failing).

3. I think this improvement would be diminished on better LLMs with built-in CoT.

4. I re-tested the 57 tasks that the ARC team measured as solved by o1-mini, and o1-mini solved 39 of them on the first try - so these are actually ‘tasks that o1-mini solves somewhat consistently’. This subset is explained by the stochasticity of LLM sampling.

I’d have liked to test o3 (no access) or o1 (too expensive) here instead. Perhaps in a paper.

5. Indeed, the first ‘top-level’ goal of ARC says:

Stay close in format to psychometric intelligence tests (while addressing issues found in previous uses of such tests for AI evaluation […]), so as to be approachable by both humans and machines.

6. We discount the fact that is definitely some 2D data in the LLM training set, such as tables and ASCII art. It’s probably harder for a model to operate on this even if it’s common in the training mix.